聊聊「二叉搜索树」的那些事儿

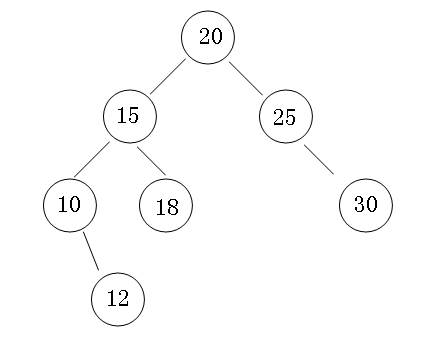
二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值； 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值； 它的左、右子树也分别为二叉排序树。“中序遍历”可以让节点有序。

原理

二叉排序树的查找过程和次优二叉树类似，通常采取二叉链表作为二叉排序树的存储结构。中序遍历二叉排序树可得到一个关键字的有序序列，一个无序序列可以通过构造一棵二叉排序树变成一个有序序列，构造树的过程即为对无序序列进行排序的过程。每次插入的新的节点都是二叉排序树上新的叶子节点，在进行插入操作时，不必移动其它节点，只需改动某个节点的指针，由空变为非空即可。搜索，插入，删除的复杂度等于树高，O(log(n))。

实现

树节点

#import <Foundation/Foundation.h>

/** 二叉树节点 */
@interface DDBinaryTreeNode : NSObject

/** 值 */
@property (nonatomic, assign) NSInteger value;
/** 左节点 */
@property (nonatomic, strong) DDBinaryTreeNode *leftNode;
/** 右节点 */
@property (nonatomic, strong) DDBinaryTreeNode *rightNode;

@end

创建

二叉排序树的创建无非就是不断查找和插入的过程，当我们查找某个值没有找到时，我们就会将该值插入到二叉排序树中。因为在查找的过程中可以确定该结点要插入的合适位置，所以插入就显得比较简单了。

#import <Foundation/Foundation.h>

@class DDBinaryTreeNode;

@interface DDBinarySearchTreeHandler : NSObject

/**
 *  创建二叉排序树
 *  二叉排序树：左节点值全部小于根节点值，右节点值全部大于根节点值
 *
 *  @param values 数组
 *
 *  @return 二叉树根节点
 */
+ (DDBinaryTreeNode *)createTreeWithValues:(NSArray *)values;

/**
 *  向二叉排序树节点添加一个节点
 *
 *  @param treeNode 根节点
 *  @param value	值
 *
 *  @return 根节点
 */
+ (DDBinaryTreeNode *)addTreeNode:(DDBinaryTreeNode *)treeNode value:(NSInteger)value;

/**
 *  二叉搜索树中某个值的节点
 *
 *  @param value	值
 *  @param rootNode 树根节点
 *
 *  @return 节点
 */
+ (DDBinaryTreeNode *)searchTreeNodeWithValue:(NSInteger)value inTree:(DDBinaryTreeNode *)rootNode;

@end

+ (DDBinaryTreeNode *)createTreeWithValues:(NSArray *)values
{
    DDBinaryTreeNode *root = nil;
    for (NSInteger i = 0; i < values.count; i++) {
        NSInteger value = [(NSNumber *)[values objectAtIndex:i] integerValue];
        root = [DDBinarySearchTreeHandler addTreeNode:root value:value];
    }
    return root;
}

添加节点

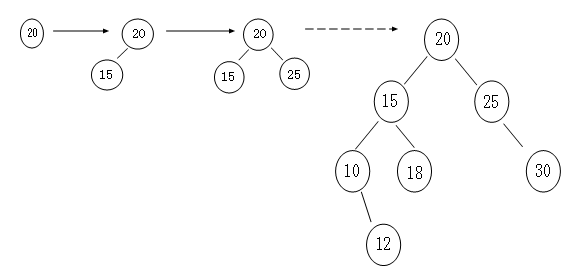
根据查找树的性质我们可以很简单的写出添加的代码，一个一个的比较，注意每插入的一个总是叶子节点。再进行调整。最终形成的效果图如下：

+ (DDBinaryTreeNode *)addTreeNode:(DDBinaryTreeNode *)treeNode value:(NSInteger)value
{
    if (!treeNode) {
        treeNode = [[DDBinaryTreeNode alloc] init];
        treeNode.value = value;
        NSLog(@"node:%td", value);
    } else if (value <= treeNode.value) {
        NSLog(@"to left");
        //值小于根节点，则插入到左子树
        treeNode.leftNode = [DDBinarySearchTreeHandler addTreeNode:treeNode.leftNode value:value];
    } else {
        NSLog(@"to right");
        //值大于根节点，则插入到右子树
        treeNode.rightNode = [DDBinarySearchTreeHandler addTreeNode:treeNode.rightNode value:value];
    }
    return treeNode;
}

查找节点

+ (DDBinaryTreeNode *)searchTreeNodeWithValue:(NSInteger)value inTree:(DDBinaryTreeNode *)rootNode
{
    if (!rootNode) {
        return nil;
    }
    
    if (rootNode.value == value) {
        return rootNode;
    }
    
    if (value < rootNode.value) {
        return [DDBinarySearchTreeHandler searchTreeNodeWithValue:value inTree:rootNode.leftNode];
    } else {
        return [DDBinarySearchTreeHandler searchTreeNodeWithValue:value inTree:rootNode.rightNode];
    }
}

删除节点

对于树来说，删除是最复杂的，主要需要考虑4种情况：叶子节点，只有左子树，只有右子树和左右子树都有。

叶子节点

删除的节点没有左子树也没有右子树，也就是删除的节点为叶子节点。这种情况下我们有可以细分为两类，一种是该叶子节点就是二叉排序树的根节点，也就是二叉排序树中只有一个节点的情况。只需要将root指针置为空即可。再一种情况是删除的叶子节点有父节点，直接将父节点连接该删除节点的指针置空即可。

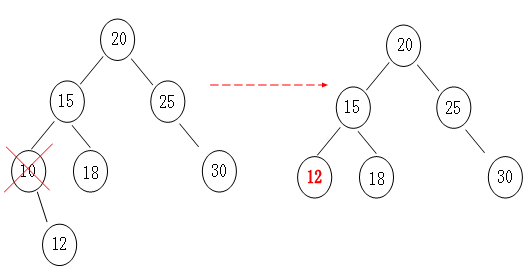
只有一个子节点

如果删除的节点有左子树那就把左子树顶上去，如果有右子树就把右子树顶上去即可。

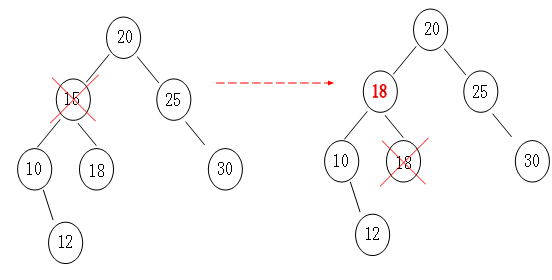
左右子树都有

首先可以这么想象，如果我们要删除一个数组的元素，那么我们在删除后会将其后面的一个元素顶到被删除的位置。

那么二叉树操作同样也是一样，我们根据”中序遍历“找到要删除节点的后一个节点，然后顶上去就行了，原理跟”数组”一样一样的。

+ (void)deleteTreeNodeWithValue:(NSInteger)value inTree:(DDBinaryTreeNode *)rootNode
{
    DDBinaryTreeNode *parent = rootNode;
    DDBinaryTreeNode *current = rootNode;
    // 记录被找到的节点是父节点的左子节点还是右子节点
    BOOL isLeftChild = false;
    // 循环直到找到目标节点的位置,否则返回
    while (current.value != value) {
        parent = current;
        if (current.value > value) {
            isLeftChild = true;
            current = current.leftNode;
        } else {
            isLeftChild = false;
            current = current.rightNode;
        }
        if (current == nil) {
            return;
        }
    }
    // 如果待删除的节点没有任何子节点
    // 直接将该节点的原本指向该节点的指针设置为nil
    if (current.leftNode == nil && current.rightNode == nil) {
        if (current == rootNode) {
            rootNode = nil;
        }
        if (isLeftChild == true) {
            parent.leftNode = nil;
        } else {
            parent.rightNode = nil;
        }
    }
    // 如果待删除的节点有一个子节点,且其为左子节点
    else if (current.rightNode == nil) {
        // 判断当前节点是否为根节点
        if (current == rootNode) {
            rootNode = current.leftNode;
        } else if (isLeftChild) {
            // 挂载到父节点的左子树
            parent.leftNode = current.leftNode;
        } else {
            // 挂载到父节点的右子树
            parent.rightNode = current.leftNode;
        }
    } else if (current.leftNode == nil) {
        if (current == rootNode) {
            rootNode = current.rightNode;
        } else if (isLeftChild) {
            parent.leftNode = current.rightNode;
        } else {
            parent.rightNode = current.rightNode;
        }
    }
    // 如果待删除的节点有两个子节点
    else if (current.leftNode != nil && current.rightNode != nil) {
        // 寻找右子树中的最小值
        DDBinaryTreeNode *successor = [DDBinarySearchTreeHandler successor:current];
        if (current == rootNode) {
            rootNode = successor;
        } else if (isLeftChild) {
            parent.leftNode = successor;
        } else {
            parent.rightNode = successor;
        }
        successor.leftNode = current.leftNode;
    }
}

/**
 在树中查找最合适的节点
 */
+ (DDBinaryTreeNode *)successor:(DDBinaryTreeNode *)node {
    DDBinaryTreeNode *successsor = nil;
    DDBinaryTreeNode *successsorParent = nil;
    DDBinaryTreeNode *current = node.rightNode;
    while (current != nil) {
        successsorParent = successsor;
        successsor = current;
        current = current.leftNode;
    }
    if (successsor != node.rightNode) {
        successsorParent.leftNode = successsor.rightNode;
        successsor.rightNode = node.rightNode;
    }
    return successsor;
}

写在最后

欢迎大家加入移动开发交流Q群交流讨论，Q群号：811237468